🔑 오늘의 학습 키워드 dp, binary search
🔗 문제링크 https://leetcode.com/problems/maximum-profit-in-job-scheduling/submissions/1360938614/
class Solution:
def jobScheduling(self, startTime: List[int], endTime: List[int], profit: List[int]) -> int:
tasks = [(s,e,p) for s,e,p in zip(startTime,endTime,profit)]
tasks.sort(key = lambda x : x[1])
dp = [(0, 0)] # (end_time, max_profit)
for s, e, p in tasks:
i = bisect_right(dp, (s, float('inf'))) - 1
current_profit = dp[i][1] + p
if current_profit > dp[-1][1]:
dp.append((e, current_profit))
return dp[-1][1]
🗒️ 공부한 내용 본인의 언어로 정리하기
🤔 문제를 보고 든 생각
dp문제라고 생각했다.
해당 시점에서 그 전에 시간까지 했던일들을 더해 나가면 되겠다고 생각을 했다.
⏰ 예상 시간 복잡도 O(N) -> 메모리 초과든 시간 초과든 날 것 같았다
Constraints:
- 1 <= startTime.length == endTime.length == profit.length <= 5 * 10 ^ 4
- 1 <= startTime[i] < endTime[i] <= 10 ^ 9
- 1 <= profit[i] <= 10 ^ 4
😎 알고리즘 개요
틀린풀이 (시간초과)
class Solution:
def jobScheduling(self, startTime: List[int], endTime: List[int], profit: List[int]) -> int:
tasks = [(s,e,p) for s,e,p in zip(startTime,endTime,profit)]
tasks.sort(key = lambda x : x[1])
max_range = max(endTime) + 1
dp = [0] * (max_range)
pointer = 0
for i in range (1,max_range):
while i == tasks[pointer][1]:
dp[tasks[pointer][1]] = max(dp[tasks[pointer][0]] + tasks[pointer][2], dp[tasks[pointer][1]])
if pointer < len(tasks) -1:
pointer += 1
else : break
dp[i] = max(dp[i-1], dp[i])
return dp[-1]
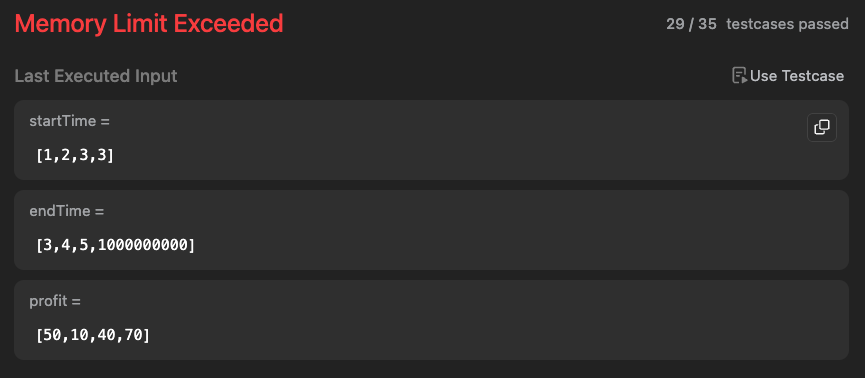
29번째 테스트케이스에서 10^9를 만났다
근데 이건 제한 조건에 의해서 사실 예상하고 있었다
-> 이분 탐색이라고 했으니 적용해서 풀어봐야겠다
-> 근데... 어디에 적용하지
-> 코드를 보니 비효율적인 부분이 많았다
개선 가능한 부분
endTime 기준으로 정렬했기에 3, 4, 5 ,다음에 나오는 10000000000 <- 이 숫자
그 사이에는 연산이 굳이 필요하지 않고 시간만 잡아먹는 6,7,8,9, --- , 99999999999가 존재한다.
이를 해결한다면 개선이 가능할 것 이라고 생각했다.
시도한 부분
1. DP를 미리 만들어두고 계산을 하면 메모리초과가 발생하기 때문에 추가하는 방법으로 해야겠다고 생각했다.
2. 이분 탐색을 활용하기 위해 해당 함수를 조사해봤다.
import bisect
dp = [(3, 50), (4, 60), (6, 100)]
startTime = 4
i = bisect.bisect_right(dp, (startTime, float('inf'))) - 1
print(i) # 인덱스 : 1
파이썬 bisect 내장 함수중에서 bisect_right는 ( 정렬된 리스트, 찾을 값, 시작 값(기본값 : 0), 끝 값 (기본값 : 마지막 값) )을 인자로 갖는다.
따라서 dp에는 ( 끝나는 시간, 그 시간에 얻을 수 있는 최대 이익) 이렇게 담겨 있기 때문에
(startTime, INF) 형태로 탐색을 해서 인덱스를 구할 수 있다.
그렇게 하면 (4, float('inf'))이 삽입될 수 있는 가장 오른쪽 위치를 찾는다.
이 인덱스는 startTime이 4일 때, 그보다 작은 endTime을 가진 항목들의 최적의 maxProfit을 가리키는 인덱스이다.
example test_case 2)
startTime = [1,2,3,4,6]
endTime = [3,5,10,6,9]
profit = [20,20,100,70,60]
Stdout
# 종료 시간순으로 정렬된 값들
[(1, 3, 20), (2, 5, 20), (4, 6, 70), (6, 9, 60), (3, 10, 100)]
# dp에 채워 나가는 값
[(0, 0), (3, 20)]
[(0, 0), (3, 20)]
[(0, 0), (3, 20), (6, 90)]
[(0, 0), (3, 20), (6, 90), (9, 150)]
[(0, 0), (3, 20), (6, 90), (9, 150)]
1. 첫 번째 작업 (1, 3, 20)
• 이 작업의 종료 시간은 3이며, 이익은 20입니다.
• bisect_right(dp, (1, float('inf'))) - 1을 통해 시작 시간이 1인 작업보다 작은 endTime을 가진 항목을 찾습니다. 이 경우 (0, 0)이 됩니다.
• 따라서 이 작업을 포함할 경우의 최대 이익은 20이 됩니다.
• dp 리스트 업데이트: [(0, 0), (3, 20)].
2. 두 번째 작업 (2, 5, 20)
• 이 작업의 종료 시간은 5이며, 이익은 20입니다.
• bisect_right(dp, (2, float('inf'))) - 1을 통해 시작 시간이 2인 작업보다 작은 endTime을 가진 항목을 찾습니다. 이 경우 (0, 0)이 됩니다.
• 따라서 이 작업을 포함할 경우의 최대 이익은 20이 됩니다.
• 이익이 이전 작업에서 구한 최대 이익 20과 동일하므로 dp 리스트는 업데이트되지 않습니다.
3. 세 번째 작업 (4, 6, 70)
• 이 작업의 종료 시간은 6이며, 이익은 70입니다.
• bisect_right(dp, (4, float('inf'))) - 1을 통해 시작 시간이 4인 작업보다 작은 endTime을 가진 항목을 찾습니다. 이 경우 (3, 20)이 됩니다.
• 이 작업을 포함할 경우의 최대 이익은 20 + 70 = 90이 됩니다.
• dp 리스트 업데이트: [(0, 0), (3, 20), (6, 90)].
4. 네 번째 작업 (6, 9, 60)
• 이 작업의 종료 시간은 9이며, 이익은 60입니다.
• bisect_right(dp, (6, float('inf'))) - 1을 통해 시작 시간이 6인 작업보다 작은 endTime을 가진 항목을 찾습니다. 이 경우 (6, 90)이 됩니다.
• 이 작업을 포함할 경우의 최대 이익은 90 + 60 = 150이 됩니다.
• dp 리스트 업데이트: [(0, 0), (3, 20), (6, 90), (9, 150)].
5. 다섯 번째 작업 (3, 10, 100)
• 이 작업의 종료 시간은 10이며, 이익은 100입니다.
• bisect_right(dp, (3, float('inf'))) - 1을 통해 시작 시간이 3인 작업보다 작은 endTime을 가진 항목을 찾습니다. 이 경우 (3, 20)이 됩니다.
• 이 작업을 포함할 경우의 최대 이익은 20 + 100 = 120이 됩니다.
• 그러나 이 값은 이미 계산된 최대 이익 150보다 작으므로, dp 리스트는 업데이트되지 않습니다.
최종 DP 리스트
최종 dp 리스트는 [(0, 0), (3, 20), (6, 90), (9, 150)]이 됩니다.
• 각 단계에서 dp 리스트는 현재 작업까지 고려한 최적의 이익을 포함하도록 업데이트됩니다.
✅ 오늘의 회고
- 똑같은 문제가 다음에 나온다고 해도 과연 풀 수 있을까 싶다.
- 이분 탐색까지 적용하는것을 생각할 수 있을까..

#99클럽 #코딩테스트준비 #개발자취업 #항해99 #TIL
'Coding test' 카테고리의 다른 글
| 99클럽 코테 스터디 31일차 TIL, 프로그래머스 / 네트워크 (0) | 2024.08.21 |
|---|---|
| 99클럽 코테 스터디 30일차 TIL, leetcode / Minimum Operations to Make a Subsequence (0) | 2024.08.20 |
| 99클럽 코테 스터디 28일차 TIL, 백준 / 스택수열 / 파이썬 (1) | 2024.08.18 |
| 99클럽 코테 스터디 27일차 TIL, 프로그래머스 / 공 이동 시뮬레이션 (2) | 2024.08.17 |
| 99클럽 코테 스터디 26일차 TIL, 프로그래머스 / 개인정보 수집 유효기간 (0) | 2024.08.16 |



